Giriş
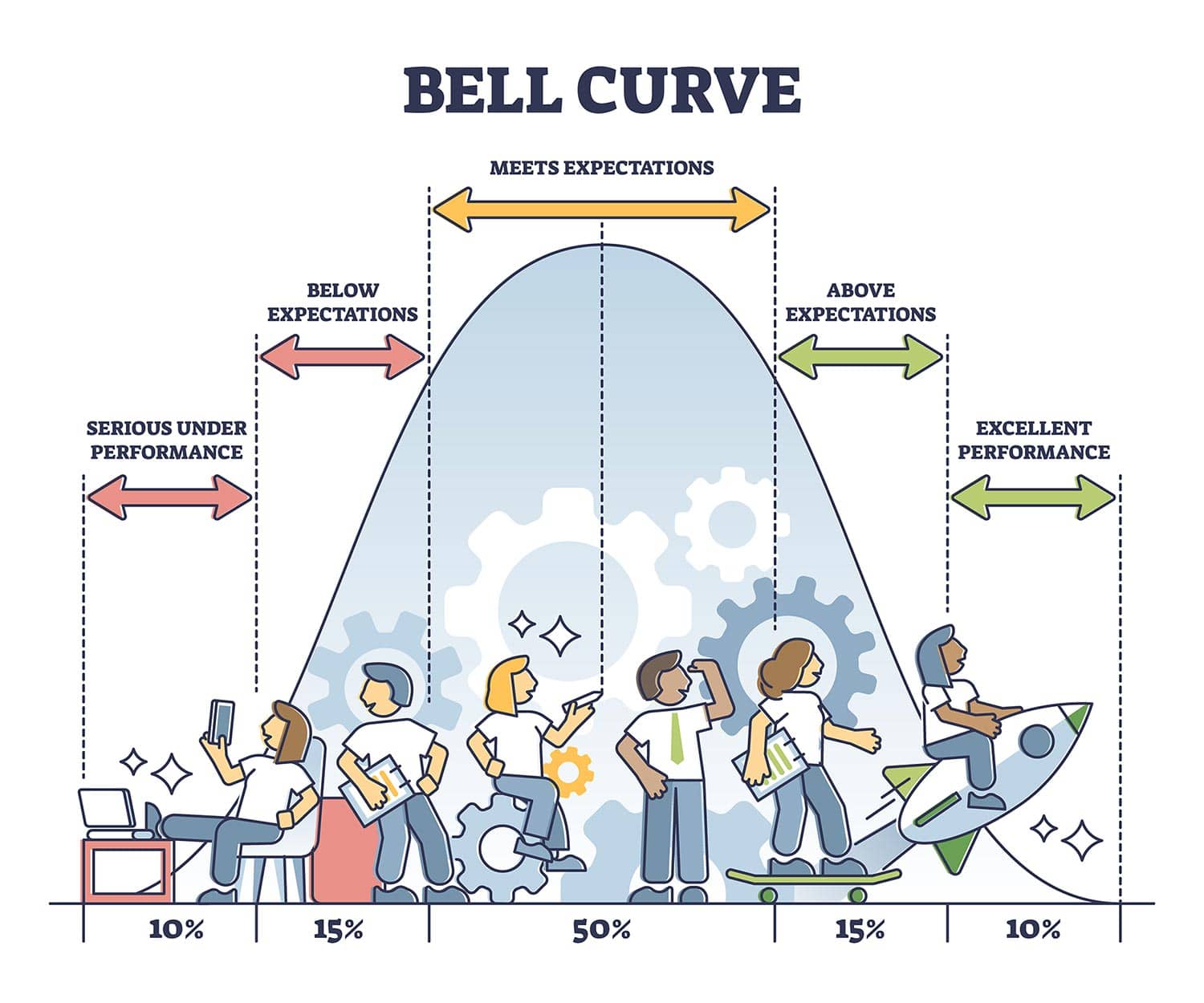
Normal dağılım, istatistik ve olasılık teorisinde merkezi bir kavramdır. Doğadaki birçok süreç ve insan faaliyetleri tarafından üretilen veriler bu dağılımı takip eder, bu yüzden “çan eğrisi” olarak da bilinir. İstatistiksel analizde, bilimde ve mühendislikte pek çok uygulaması vardır. Bu makale, normal dağılımın temellerini, matematiksel özelliklerini ve çeşitli alanlardaki uygulamalarını inceleyecektir.
Normal Dağılımın Tanımı ve Özellikleri
Normal dağılım, sürekli olasılık dağılımıdır ve simetrik, tek zirveli, çan şeklinde bir eğriye sahiptir. Matematiksel olarak, normal dağılımın yoğunluk fonksiyonu şöyle ifade edilir:
[ f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{ -\frac{(x-\mu)^2}{2\sigma^2} } ]Burada ( \mu ) ortalama veya beklenen değeri, ( \sigma ) ise standart sapmayı temsil eder. Bu iki parametre, dağılımın şeklini ve yerini tanımlar: ( \mu ) eğrinin merkezini belirlerken, ( \sigma ) eğrinin genişliğini ve yayılımını kontrol eder.
Temel Özellikler
- Simetri: Normal dağılım, ortalaması olan ( \mu ) etrafında simetrik bir yapıya sahiptir.
- Asimptotik: Eğri, hem sağda hem solda sonsuza doğru uzanır, ancak eksenlere değmez.
- Empirik Kural (68-95-99.7 Kuralı): Verilerin yaklaşık %68’i ortalama etrafında bir standart sapma içinde, %95’i iki standart sapma içinde ve %99.7’si üç standart sapma içinde yer alır.
Uygulamaları
Normal dağılımın en belirgin uygulamalarından biri standart skorların hesaplanmasıdır. Z skorları, bir gözlemin ortalama etrafında ne kadar uzakta olduğunu standart sapmalar cinsinden ifade eder ve şöyle hesaplanır:
[ z = \frac{(x - \mu)}{\sigma} ]Bu dönüşüm, farklı ortalama ve standart sapmalara sahip veri setlerinin karşılaştırılmasını sağlar.
Normal Dağılımın Sınırlamaları
Her ne kadar birçok doğal ve sosyal fenomeni modellemek için uygun olsa da, normal dağılım her veri kümesi için uygun değildir. Özellikle, aşırı değerler (outliers) veya asimetrik veriler için uygun olmayabilir. Bu tür durumlarda, log-normal dağılım, üstel dağılım veya diğer dağılımlar daha uygun olabilir.
Normal dağılım, teorik açıklıkları ve pratik uygulamaları ile istatistikte vazgeçilmez bir araçtır. Temel özelliklerinin anlaşılması, veri analizi ve çıkarımsal istatistikte sağlam bir temel sağlar. Ancak, her analitik durum için evrensel çözüm olmadığını anlamak önemlidir ve veri setinin karakteristiklerine uygun modellerin seçilmesi gerekir. Verilerin doğasını dikkatlice değerlendirerek ve uygun istatistiksel testler uygulayarak, analistler daha doğru ve güvenilir sonuçlar elde edebilirler.
Normal dağılım, istatistik ve çeşitli bilim dallarında pek çok farklı şekilde kullanılır. İşte normal dağılımla ilgili birkaç uygulamalı örnek:
- Psikolojide Zeka Testleri: Zeka testleri, genellikle zeka puanlarının normal dağılımda olduğu varsayılır. Bu, çoğu insanın ortalama bir zeka puanına sahip olduğunu, çok düşük veya çok yüksek zeka puanına sahip insan sayısının ise az olduğunu gösterir. Örneğin, IQ testlerinde ortalama puan genellikle 100 olarak belirlenir ve standart sapma 15 olarak kabul edilir. Bu, toplumun yaklaşık %68’inin 85 ile 115 arasında bir IQ puanına sahip olduğu anlamına gelir.
- Hata Ölçümleri: Mühendislikte, ölçüm hataları genellikle normal dağılımı takip eder. Bu, ölçümlerdeki küçük hataların sık, büyük hataların ise nadir olduğu anlamına gelir. Örneğin, bir parçanın üretim toleransı belirli bir süreçte normal dağılımla analiz edilebilir, bu da üretim kalitesinin kontrol altında tutulmasına yardımcı olur.
- Tıpta Kan Basıncı ve Diğer Biyolojik Ölçümler: İnsanlarda kan basıncı gibi birçok biyolojik ölçüm normal dağılıma uyar. Normal sağlıklı yetişkinlerin çoğu belirli bir aralıkta kan basıncına sahiptir ve çok yüksek veya çok düşük değerler daha az sıklıkta görülür.
- Finansta Stok Getirileri: Ekonomi ve finansta, stok getirileri bazen yaklaşık olarak normal dağılımla modellenebilir, özellikle kısa süreli getiriler için. Bu, risk yönetimi ve finansal modelleme açısından önemlidir çünkü normal dağılım, olası getiri dağılımını tahmin etmek ve portföy stratejileri oluşturmak için kullanılabilir.
- Kalite Kontrolü: Üretim süreçlerinde, ürün boyutları ve ağırlıkları gibi özellikler normal dağılımı takip edebilir. Bu, üretim hatasını azaltmak ve süreç kapasitesini değerlendirmek için kalite kontrolünde istatistiksel yöntemlerin kullanılmasını sağlar.
Bu örnekler, normal dağılımın geniş kullanım alanlarını ve çeşitli disiplinlerdeki uygulamalarını göstermektedir. Normal dağılım, teorik kolaylığı ve pratikteki uygulanabilirliği nedeniyle pek çok alanda vazgeçilmez bir araçtır.
Bir kaç basit uygulama ile çalışalım;
Soru:
Bir üniversite sınavında matematik puanlarının normal dağılımda olduğu ve ortalamanın (μ) 70, standart sapmanın (σ) ise 10 olduğu biliniyor. Öğrencilerin %16’sının aldığı puanın 80 veya daha fazla olduğunu bulun.
Çözüm:
Normal dağılım için z skoru formülü şudur:
[ z = \frac{X – \mu}{\sigma} ]
Burada ( X ) ilgilendiğimiz puan, ( \mu ) ortalama ve ( \sigma ) standart sapmadır.
- z Skoru Hesaplama:
Bizden istenen öğrencilerin %16’sının aldığı puanın 80 veya daha fazla olduğu. Bu, z tablosu veya normal dağılım tablosunu kullanarak tersine çözmemiz gereken bir durumdur. Normalde, z tabloları sol kuyruktaki alanı verir, ancak biz sağ kuyruğu, yani %16’lık kısmı arıyoruz. z tablosunda %16’lık kısım, normalde %84’lük kümülatif olasılığa denk gelir (çünkü %100 – %16 = %84). Z-tablosu veya hesap makinesi kullanarak, %84’ü veren z değerini bulmamız gerekiyor. %84’ü veren z skoru yaklaşık olarak +1.00’dır (z tablosuna veya bir hesap makinesine bağlı olarak küçük farklar olabilir). - Puanı Hesaplama:
Bu z skorunu kullanarak gerçek puanı bulabiliriz. z formülünü ( X ) için çözeriz: [ X = \mu + z\sigma ]
[ X = 70 + (1.00)(10) ]
[ X = 70 + 10 ]
[ X = 80 ]
Bu hesaplama, eğer bir öğrencinin puanı 80 veya daha yüksekse, bu puanların öğrenci popülasyonunun yaklaşık %16’sına denk geldiğini doğrular.
Sonuç:
Bu örnek, normal dağılımın ve z skorunun nasıl kullanılacağını ve gerçek dünya verilerini nasıl yorumlayabileceğimizi göstermektedir. Öğrencilerin %16’sının 80 veya daha yüksek bir puan aldığını ve bu tür bir sorunun çözümünde normal dağılımın nasıl kullanılacağını anlamamızı sağlar.
Tabii, işte biraz daha karmaşık bir normal dağılım problemi:
Soru:
Bir iş yerinde çalışanların aylık gelirleri normal dağılımda olduğu ve ortalamanın (μ) 5000 TL, standart sapmanın (σ) ise 800 TL olduğu biliniyor. Bir çalışanın rastgele seçilip aylık gelirinin 6000 TL’den fazla olma olasılığını ve 3000 TL’den az olma olasılığını hesaplayın.
Çözüm:
- 6000 TL’den Fazla Olma Olasılığı: İlk adım, 6000 TL için z skorunu hesaplamaktır:
[ z = \frac{X – \mu}{\sigma} ]
[ z = \frac{6000 – 5000}{800} ]
[ z = \frac{1000}{800} ]
[ z = 1.25 ] z skoru 1.25 için, z tablosundan veya normal dağılım hesaplayıcısından kümülatif olasılığı bulmalıyız. Bu değer genellikle yaklaşık 0.8944’tür, yani %89.44. Bu, seçilen bir çalışanın 6000 TL veya daha az kazanma olasılığını gösterir. Ancak biz 6000 TL’den fazla kazanma olasılığını istiyoruz: [ P(X > 6000) = 1 – P(X \leq 6000) ]
[ P(X > 6000) = 1 – 0.8944 ]
[ P(X > 6000) = 0.1056 ] Yani, bir çalışanın aylık 6000 TL’den fazla kazanma olasılığı yaklaşık %10.56’dır. - 3000 TL’den Az Olma Olasılığı: Şimdi, 3000 TL için z skorunu hesaplayalım:
[ z = \frac{3000 – 5000}{800} ]
[ z = \frac{-2000}{800} ]
[ z = -2.5 ] z skoru -2.5 için, z tablosundan veya hesaplayıcıdan kümülatif olasılığı bulmalıyız. Bu değer genellikle yaklaşık 0.0062’dir, yani %0.62. Bu, seçilen bir çalışanın 3000 TL veya daha az kazanma olasılığını gösterir: [ P(X < 3000) = 0.0062 ] Yani, bir çalışanın aylık 3000 TL’den az kazanma olasılığı yaklaşık %0.62’dir.
Sonuç:
Bu örnek, normal dağılımı kullanarak gelir dağılımı gibi gerçek dünya verilerini nasıl analiz edebileceğimizi gösterir. Çalışanların gelir dağılımını anlamak, iş yerinde maaş politikaları ve ekonomik eşitsizlikler üzerine tartışmalar için önemli olabilir.